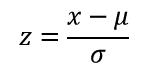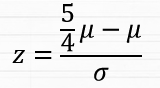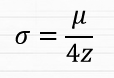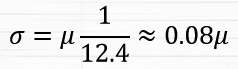WoT w sposób matematyczny – rozkład obrażeń

Matematyka to potężne narzędzie. Przez liczby, ich stosunki i działania można określić praktycznie każdy aspekt naszego życia. Dziedzina ta przydaje się w płaceniu za produkty, obliczaniu potrzebnych nam zadań czy zliczaniu postów od hejterów pod naszymi artykułami 🙂 Dlatego więc zapaleńcy matematyczni tak chętnie sięgają po swoją liczbową wiedzę, badając różne kwestie związane z naszą ulubiona grą – World of Tanks!

Takiego zadania podjął się jeden, z graczy WoT-a, redditor – Dae314. Przeprowadził on eksperyment, który miał na celu wskazanie najlepszego parametru matematycznego, którym można określić Rozrzut Obrażeń w World of Tanks – dalej nazywane ROWOT 🙂 Otóż ROWOT jest parametrem, który każdy chyba chciałby znać i wiedzieć, jak jego zależność wpływa na nasze umiejętności i, ogólnie, na naszą grę. Zacznijmy więc od początku i przeanalizujmy, co „poeta miał na myśli”…

Już na samym początku materiału autor stwierdza, że według jego ustaleń, najlepszym parametrem do obliczania ROWOTa jest parametr nazwany sigma, i mający wartość 3.1. Swoje badania oparł na próbce ponad 1000 losować obrażeń w grze. Za czołg wzorcowy posłużył poczciwy T110E5 (średnie obrażenia 400, min 300, max 500). Dae314 nałożył też pewne obostrzenia na eksperyment:

• pod uwagę nie były brane blow-upy (wybuch magazynu amunicji)
• nie używał pocisków typu HE (odłamkowo-burzących)
• nie liczył strzałów w pojazdy, które miały mniej, niż 500 punktów życia.

Zacznijmy może od tego, co autor ma na myśli przez wskaźnik sigma = 3.1 (uwaga, będzie sporo zwrotów matematycznych :P). Otóż autor zaczął analizę od wyprowadzenia najlepszego parametru, który zlicza maksymalne obrażenia pojazdu. Parametrem tym okazała się standaryzacja Z, którą oblicza się ze wzoru:

gdzie: x- maksymalne obrażenia, zadane przez pojazd; m – średnie obrażenia pojazdu; b – odchylenie standardowe.

Ok, parametr x oraz m (specjalnie użyłem uproszczonej symboliki – proszę purystów językowych o nie czepianie się :P) są w miarę zrozumiałe, ale pewnie nie każdy wie co to odchylenie standardowe. Otóż przez ta miarę oznacza się jak szeroko wartości jakiejś wielkości (w naszym przypadku obrażenia zadane przez czołg) są rozrzucone wokół jej średniej. Im mniejsza wartość odchylenia tym obserwacje są bardziej skupione wokół średniej [źródło: wikipedia.pl]. I w skrócie, właśnie to odchylenie, tak na prawdę, odpowiedzialne za Rozrzut Obrażeń w World of Tanks. No ale co z tą standaryzacją Z? O tym za chwilę. Teraz przechodzimy więc do czystych statystyk.

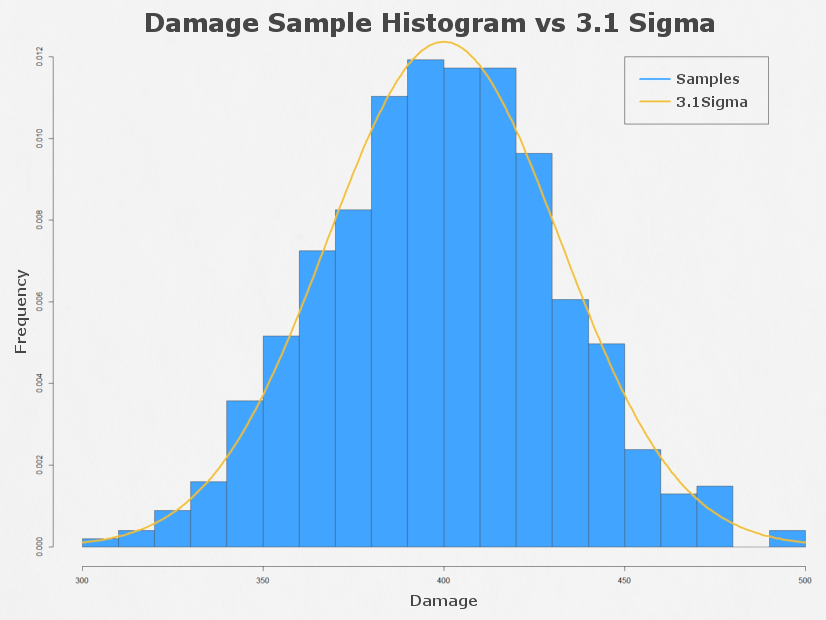
Badanie, jakie przeprowadził autor, wykazało, że średnie obrażenia, jakie zadawał czołg, wyniosły 399,99. Odchylenie standardowe było równe 32,39, zaś ilość próbek, jak pamiętacie z początku artykułu, równa 1006.

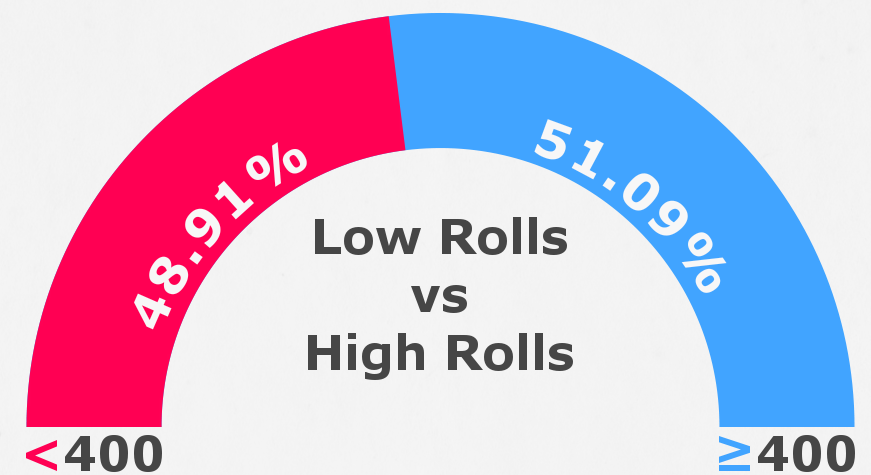
Dodatkowo test pokazał, w jaki sposób rozkładają się obrażenia (niski roll i wysoki roll):

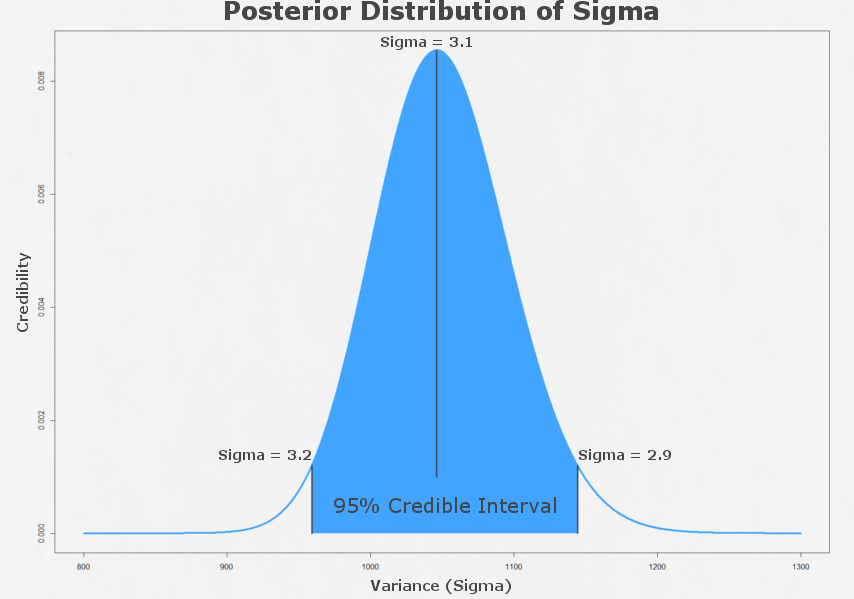
To wszystko pozwoliło stworzyć wykres zależności wiarygodności parametru od jego wariancji, którego treść opiera się na działaniu Statystyka w ujęciu Bayesowskim (szkoda czasu na rozpisywanie się, zerknijcie w link :P).

Co widzimy na wykresie? Otóż to, że 95% wartości wariancji mieści się w przedziale między 2.9 a 3.2, z czego 3.1 jest wartością, która najbardziej odpowiada histogramowi stosunku obrażeń do częstości występowania:

Tyle z wykresików, sigm i innego graficznego łatajstwa. Wracamy do tematu standaryzacji Z. Przejdźmy po kolei przez poszczególne etapy obliczania. Przypominam wzór:

Zaczynamy od postawienia za x wartość maksymalnych obrażeń. W grze są to średnie obrażenia pomnożone przez współczynnik 1,25 (widełki +/- 25%):

Dokonując szybkich przeliczeń (obliczenie z, a następnie wyciągnięcie z tego odchylenia), otrzymujemy wzór:

Przy założeniu, że standaryzacja Z jest dla wszystkich czołgów jednakowa, możemy podstawić za nią naszą wartość sigmy, wziętej z wykresu, czyli 3.1. Daje nam to wynik:

Przekładając na język polski – autor wykazał, że zależność parametru odchylenia standardowego jest zależne od średnich obrażeń czołgu. Dzięki temu można wykazać (wiedząc, że rozkład obrażeń określa krzywa Gaussa, czyli rozkład normalny), że, np.:

• 68% strzałów będzie zawierało wartość w widełkach 8% średnich obrażeń
• 98% strzałów będzie zawierało wartość w widełkach 16% średnich obrażeń

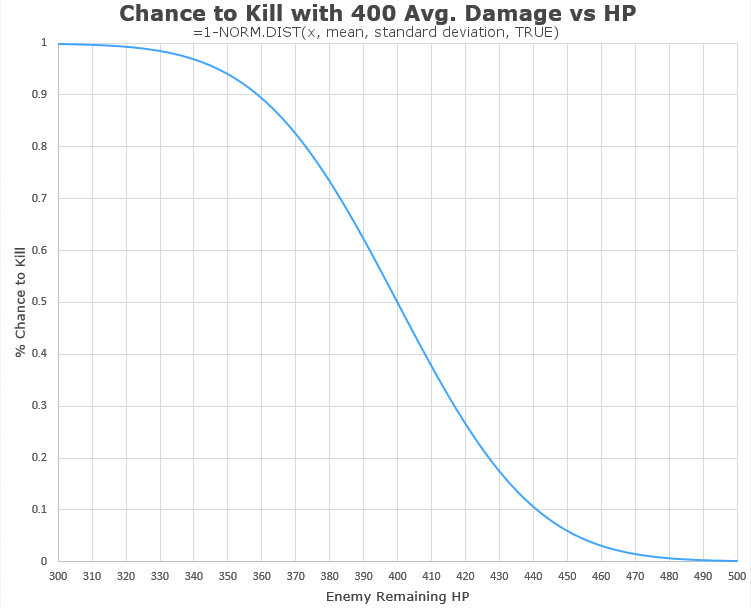
Wiedza ta pozwala też zasymulować wykres stosunku szans ubicia czołg w zależności od jego ilości HP:

Widać na nim, że szanse ubicia pojazdu (jednym strzałem z działa naszej E5) z ilością życia równe 400 HP wynoszą fifty-fifty (50%). Jeszcze mniejsze szanse mamy na zabicie pojazdu z 410 punktami życia – tylko 37.8%, a więc prawie jedną trzecią. To może dać Wam też do zrozumienia, dlaczego czołgi przeżywają nasze na groszowych ilościach życia 🙂

Na tym się kończy wykład profesora Dae314. Warto wspomnieć, że wcześniej również przeprowadził taki eksperyment, tym razem dla simgy równej 2.5. Prócz tego autor tekstu ciągle bada, czy standaryzacja Z jest taka sama dla wszystkich pojazdów, a to mu się jeszcze zejdzie 🙂

Jeżeli chcecie zobaczyć oryginał tekstu badania, które dostępne na Reddicie, kliknijcie w ten link.

Źródło: KLIK

Cała Infografika: